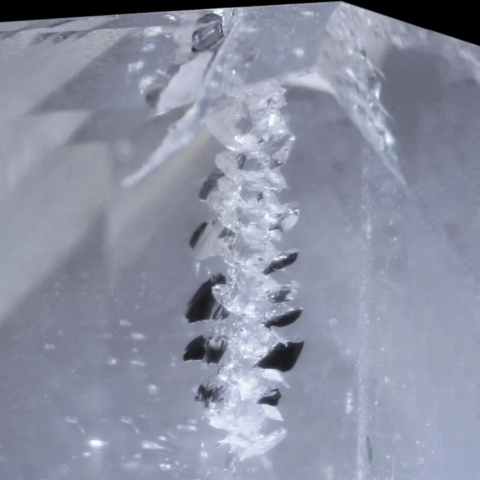
The mystery of helical inclusions in beryls
Beryls and spodumenes are prized minerals in mineralogy and gemology, particularly for their colored varieties such as emerald and aquamarine (beryl) or kunzite (spodumene). In some localities, these crystals exhibit helix-shaped inclusions, an intriguing feature that may result from the Liesegang phenomenon. This article explores how this chemical mechanism of periodic precipitation might explain these singular formations.
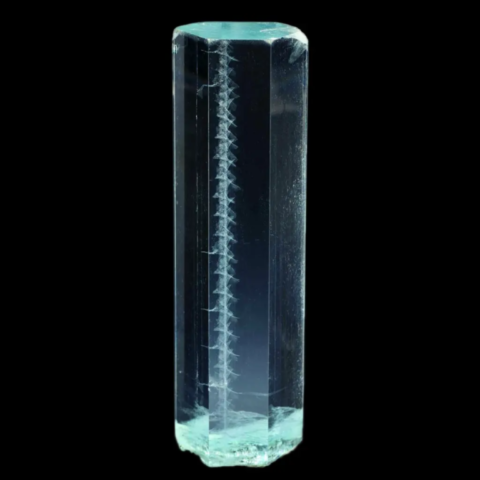
Photo : Aquamarine with helical inclusions from Minas Gerais, Brazil © Jeff Scovil
What is the Liesegang phenomenon ?

Discovered in 1896 by chemist Raphael Eduard Liesegang, this phenomenon describes the spontaneous formation of periodic patterns—such as rings, bands, or striations—during chemical reactions in a medium where a substance diffuses slowly. Typically observed in gels, this process relies on an instability mechanism : when a diffusing reactant locally reaches a critical concentration, it reacts abruptly with another component of the system, causing the formation of a precipitate. This local reaction depletes nearby reactants, preventing the immediate formation of a new precipitate until the concentration increases further. This repeating cycle generates structures regularly spaced in time and space.
Translated to the crystalline context, a similar mechanism could explain the formation of periodic fluid inclusions in minerals such as beryl or spodumene. During crystal growth, the latter is bathed in fluids rich in dissolved elements. If local chemical conditions (pressure, temperature, concentration) sometimes favor the imprisonment of these fluids rather than their evacuation or reaction, this would result in the formation of fluid inclusions at regular intervals. This rhythmic trapping, governed by a Liesegang-type mechanism, would give rise to organized patterns within the crystal itself.
Right photo : Formation of a silver dichromate precipitate in gelatin in a Liesegang patterns © Büki András & Oláh Zsuzsa
The Liesegang phenomenon and its theories
The Liesegang phenomenon is based on the complex interaction between the diffusion of chemical species and localized reactions subject to critical thresholds. When a diffusing reactant encounters another substance in sufficient concentration, a sudden reaction occurs (often precipitation), generating discontinuous and periodic structures, such as rings or bands, in the medium. The regular spacing of these structures results from the alternation between active zones (where the reaction is possible) and inhibited zones (where the reactants have been consumed).
One of the classic models proposes that the reaction only begins when the concentration of a reactant exceeds a certain supersaturation threshold, which explains the periodicity. Another, more complex model introduces the idea of diffusing intermediates : intermediate products (chemical complexes, colloids, etc...) form during the reaction and facilitate the propagation of the process over distances, reinforcing the periodicity.
In the case of fluid inclusions observed in crystals such as beryls or spodumenes, these models can be adapted. Here, the fluid is not precipitated, but trapped at specific locations in the crystal, probably when certain thermodynamic conditions are met. If crystal growth is continuous and directional, and if the growth front interacts with a slowly diffusing fluid, periodic fluid trapping may occur, following a logic similar to that of the Liesegang phenomenon.
Finally, some theories suggest the formation of concentration waves or periodic perturbations in the growth front, which could generate even more complex patterns, such as spirals or helices. In a crystal that preferentially grows along one axis (such as the c axis of beryls), such perturbations can be distorted and driven into a helical motion, which would explain the spiral arrangement of fluid inclusions.

Formation of helical inclusions by the Liesegang mechanism :
In crystals such as beryl or spodumene, the formation of fluid inclusions arranged in a helix can be interpreted in light of the Liesegang phenomenon, and more specifically, via the diffusing intermediates model. These minerals form in hydrothermal or pneumatolytic environments, where crystal growth occurs directly in contact with a hot fluid rich in dissolved elements (lithium, beryllium, iron, etc...). As the crystal grows, it interacts with this fluid, and certain local conditions can lead to the periodic entrapment of small pockets of fluid, thus creating inclusions.
According to the diffusing intermediates model, intermediate chemical species (such as ionic complexes or unstable aggregates) can temporarily alter the diffusion rate of elements into the surrounding fluid. This creates zones where growth is locally slowed or accelerated, favoring the rhythmic entrapment of small amounts of fluid within the crystal. These inclusions therefore do not form randomly, but according to a periodicity governed by the physicochemical conditions of the system.
The particular geometry of these helical inclusions can be explained by the directional growth of the crystal, particularly along its c-axis, which is often the preferred growth axis. As the crystal elongates, the inclusions trapped in a periodic pattern are gradually drawn into a spiral motion, either by a slight misalignment of the growth front or by the presence of dislocations or disturbances in the structure. The original pattern (regular and linear) is thus transformed into a three-dimensional spiral.
In the experiments described by Shibi Thomas & al. (2013), the formation of helical patterns in gel tubes strongly depends on the tube diameter: below a certain critical size, only classical precipitation bands appear, while above this threshold, well-defined helices can emerge. The winding direction of these helices (right-handed or left-handed) appears completely random, as the system has no initial chirality that can impose a direction. This phenomenon results from a spontaneous symmetry breaking, where small perturbations are amplified during the process. Finally, local variations in the fluid, such as micro-fluctuations in temperature, composition, or pressure, can accentuate the complexity of the structures formed. This would explain why some inclusions take on particularly irregular or helical shapes: they reflect a dynamic and sensitive process, combining directional crystal growth, fluid-crystal interaction, and diffusion instabilities.
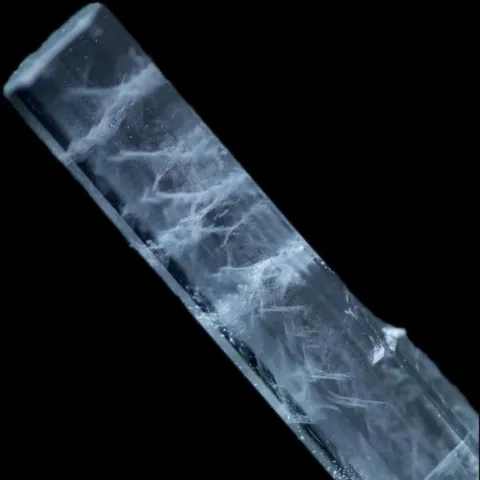
Photo : 7 cm aquamarine with helical inclusions from Shigar, Pakistan © Mineral Masterpiece

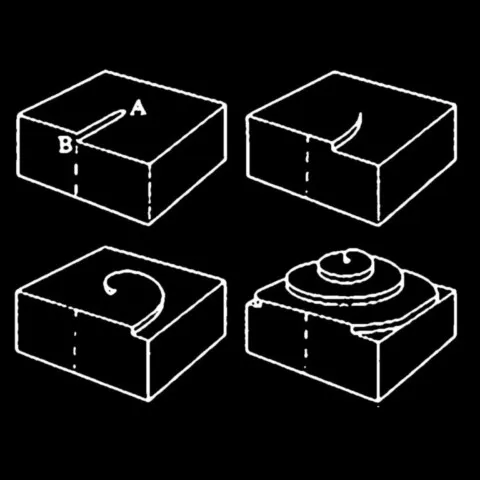
A smaller-scale process : screw dislocations
Another mechanism that could explain helical inclusions is screw dislocations. These crystal defects appear when crystal growth is disrupted by local deformation, creating a spiral structure that guides crystallization.
In this scenario, helical inclusions would not only be the result of Liesegang diffusion and precipitation, but also of a spiral movement of crystallizing atoms around a dislocation. This process could act in conjunction with the Liesegang phenomenon, producing a complex structuring of inclusions at both the macroscopic and microscopic scales.
Diagrams and photo : Diagrams of a screw dislocation and photo of a screw dislocation around a fluorite twin from Rogerley, United Kingdom © Rémi Bornet
Why are beryls and spodumenes affected ?
Beryls and spodumenes are particularly susceptible to helical fluid inclusions due to the specific geological conditions in which they form. These minerals typically crystallize in pneumatolytic or hydrothermal environments, located at the interface between the final phases of magmatic differentiation and hot fluid circulation. These environments are rich in volatile elements (fluorine, boron, water, etc.) and light elements such as lithium and beryllium, which favors both mineral growth and fluid incorporation.
These conditions are often unstable, with variations in temperature, pressure, and chemical composition that can lead to saturation and precipitation cycles. This creates a favorable environment for periodic fluid trapping, similar to the Liesegang phenomenon.
Furthermore, beryls and spodumenes exhibit marked directional growth, particularly along their crystallographic c axis. When a fluid inclusion pattern forms regularly, this axial growth can lead to a progressive coiling of the pattern, transforming a linear distribution into a helical structure.
The presence of mobile elements such as lithium, beryllium, or iron can also promote complex diffusion processes, sometimes accelerated by the formation of intermediate complexes in the fluid, contributing to a modified periodic precipitation pattern. Finally, the presence of screw dislocations, common in large crystals, can reinforce or induce this spiral structuring by serving as a helical growth channel.
Note that helical inclusions are also known in other mineral species such as topaz, tourmaline, and natrolite.
Conclusion
The hypothesis that the helical inclusions observed in certain beryls and spodumenes result from the Liesegang phenomenon is a plausible explanation. By combining chemical diffusion, periodic precipitation, and anisotropic growth, this model allows us to interpret these fascinating patterns from a chemical and crystallographic perspective.
Furthermore, the presence of screw dislocations could act at a finer scale, influencing the formation of helical structures. This coupled phenomenon could open new avenues of research into the origin of these inclusions.
Future studies could explore this hypothesis by simulating growth conditions and analyzing the chemical composition of the inclusions to confirm their Liesegangian nature.
References :
KAI S., MÜLLER S. C., ROSS J. (1983). Periodic Precipitation Patterns in the Presence of Concentration Gradients. 2. Spatial Bifurcation of Precipitation Bands and Stochastic Pattern Formation. Journal of Physical Chemistry, 87(13), 2404-2410.
LIESEGANG, R.E. (1896). Ueber einige Eigenschaften von Gallerten. Naturwissenschaftliche Wochenschrift, 11, 353–362.
MÜLLER S. C., KAI S., ROSS J. (1982). Curiosities in Periodic Precipitation Patterns. Science, 216 (4546), 635-637
MÜLLER S. C., KAI S., ROSS J. (1982). Periodic Precipitation Patterns in the Presence of Concentration Gradients. 1. Dependence on Ion Product and Concentration Difference. Journal of Physical Chemistry, 86 (6), 903-909.
OSTWALD, W. (1897). Studien über die Bildung und Umwandlung fester Körper. Zeitschrift für physikalische Chemie, 22, 289–330.
THOMAS S., LAGZI I., MOLNÁR F. Jr., RÁCZ Z. (2013). Helices in the wake of precipitation fronts. Physical Review E, 88(2), 022141